| 19.4. Remove Jumps | ||
|---|---|---|
 | Chapter 19. Debrief algorithms | 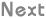 |
![[Note]](images/note.gif) | Note |
|---|---|
|
Read the user perspective on removing jumps in the user guide (Section 3.7.7, “Removing Jumps”) |
The initial strategy to remove drift was to find the range/direction of the jump from the last dived point to the first GPS fix. But, during implementation it became clear that this wouldn't work. What was actually needed was to "plot-on" the last dived point to derive where the dived track would be at the time of the GPS fix. The following diagram shows a stylized representation of a period of dived drift.
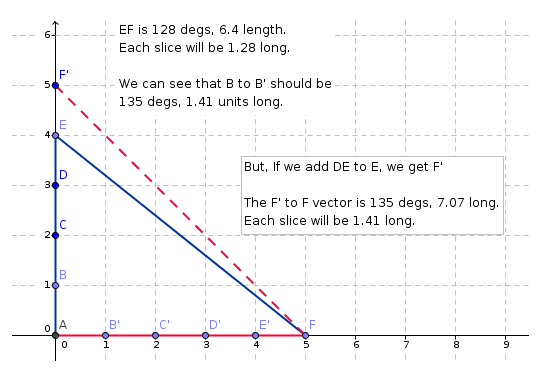
In the diagram, the measured track is AEF, but the true track was AF. We can see that the correct location for B is B', C is C', and so on. So, the vector necessary to transform B to B' is 135 degs length 1.41 (sqrt(2)). This correct vector can be obtained by producing the virtual point F', which is defined as “where would F be if there hadn’t been a jump”. Using F'-F as the offset vector gives the correct result.
Analyst selects period of data.
The first position is stored as a “lock point”.
Loop forwards through data, looking for large position deltas (where calculated speed equates to 3 or more time the measured speed travelled in the previous step).
Each time we find a jump, the position after the jump is a “lock point”, the position before jump is the “jump point”. The delta between the two is the “jump offset”.
From the first lock-point, move forwards through the data until you find a jump point. If a jump point is found, pass through those points, applying the relative sliced jump offset to each point.
The diagram belows shows the results of remove jumps. The yellow track ABCDEFG is the recorded track. The points A,C,E,G are the lock-points (GPS fixes). The blue track is the track after running remove jumps. Note that AC is longer than AB, so the algorithm has rotated and scaled AB. Similarly, CE is shorter than CD and gets scaled to produce CE. EG shows how a complex shape gets transformed to fit the lock points.